ある閉じた(境界がない)曲面を考えます。
例えばこんなん。

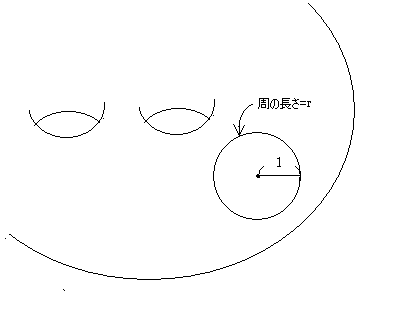
実は、この積分の値は曲面を多少引っ張ったりちぢめたりして再度計算しても変わりません。
このことを、この積分値は位相的に不変であるといいます。
位相的に不変な量のことを位相不変量とよんだりします。
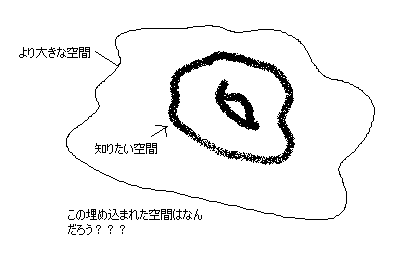
ある空間の位相不変量は、それが他の適当な空間(ある高次元の空間)に埋め込まれている場合も変わらないので、
その場合に埋め込まれた空間上の積分が実行できれば、
この曲面がどういうものか(例えば球面なのかドーナツなのか)が判別できることになります。
話を元に戻すと、この積分値は-2πの整数倍でありその整数は曲面のオイラー数(注2)に等しくなります。 この事実をガウスボンネの定理(もしくは公式)といいます。
球面が3次元空間に埋め込まれている場合を考えましょう。
丁度宇宙空間を漂う地球の表面のように(でもできる限り滑らかであると考えてください)。

では、ドーナツの表面ではどうでしょうか? 実はドーナツの表面のオイラー数が0です。 逆に、ガウスボンネの定理からさっきの積分値は0になるはずですね。 このことを考えてみてください。 また、どこにも裂け目ができないようなドーナツはあるでしょうか?
(このパラグラフは少し専門的になります。すいません^^;)
これらのことは大学で幾何学を少しでも学習した人なら、曲面上の接束の半径1の大域角形式が
マイナス1倍のオイラークラス(単位接球面束のオイラークラス)の引き戻しであると理解していると思います。
この事実は曲面上に限らず勝手な多様体(注3)上で定義され、主張できるものです。

積分される被積分関数は位相幾何的対象ではありませんが、積分をして初めて位相不変量になります。 位相幾何学はこのような位相不変量を使ってもっと高次元の物体(主に多様体)を構成したりその性質を調べたり、 あるいはある性質を満たす位相不変量(量子不変量やゲージ理論不変量などがあります)の性質を調べたりします。 ちなみに上記の被積分関数や曲率(曲がり方)などを研究するのは微分幾何学とよばれる位相幾何学とは別の幾何学に属します。
(さいごに) 位相幾何学を研究するには、位相不変量だけではできません。 位相幾何学はそれ自体''上っ面の幾何学"であり、その性質をきちんと理解するためには 背後に潜むもう少し複雑なメカニズムに着目しなければなりません。 こうした連携が研究では重要になってきます。 例えば、最近話題になっているポアンカレ予想も位相幾何学の命題ですが、その背後にある微分幾何学を統計物理学的に扱うことで 解決されました。
(注1)ここでの積分法とは、以下の方法のことをいいます。 曲面をいくつかのピースに分割をしてそのピースに含まれる点上の関数をとるような棒グラフ的な関数を 考えます。 その棒グラフの体積(底面はそのピースの面積、高さは棒の長さ)を曲面全体で足し合わせることで ある値が算出されます。 求める値はこうして得られた値を、より細かい分割を使って (正確にはより直径の小さいピースになるように)得られた値の分割に関する極限です。 実はこうして得られる値は極限に向かう分割の仕方によらず求まります。 これは一般にリーマン積分とよばれており、高校の教科書にある区分求積法は この事実を用いて計算される積分法のひとつです。
(注2)曲面を3角形でタイル張りをします。 つまりどこでも3角形が重ならないように、2つの3角形の共通部分はあっても1点か1辺のみ。 このタイル張りに含まれる点の数、引く辺の数、足す面の数として定義される整数をその曲面のオイラー数といいます。 この数はタイル張りの仕方によらない位相不変量です。 例えば、球面は2、ドーナツの表面は0、ドーナツをn個くっつけた曲面の表面は-2n+2。 ですからこの話の最初に登場した曲面のオイラー数は-2ということになります。
(注3)n次元多様体とは滑らかな曲面を高次元に拡張した幾何学的対象。 滑らかとは、その対象を十分近くで見ると(ズームインしていくと)その次元の線形空間が見えてくること。
(1/6/2011)4次元ってなんでしょうか?
まず、3次元空間とはなんでしょうか。
次元とは、ものの広がり方を表していて、
この下の絵のように、左に立っている人間は広がり方に幅、奥行き、高さがあり見た目、3次元です。

例えば、大まかに見れば、人間はほぼ、地表を歩いているだけの動物です。 でも、空飛ぶ鳥は地表も歩くこともできますし、空中も自由自在です。 人間は2次元に住む動物で、鳥は3次元に住む動物と考えることができます。 1次元に住んでいる動物はいるでしょうか?(みみずはどうか?)
では、改めて4次元を考えてみます。 3次元は空間の広がり方3種類だったから、4次元では4種類の広がり方を考えればよいということになります。 新しい方向を追加しなければなりません。 それはどこにあるのでしょうか?この世の中には新しい方向はもうありません。 その新しい方向はこの3次元の世の中には見えない方向を指しているのですが。。。 ドラえもんの4次元ポケットに入ると、吸い込まれるようにどこかに消えてしまいますね。 つまり、どこか見えない空間に入ってしまうわけです。 それが新しい方向です。
見えないというのは3次元から見ているからで、4次元ではきっと普通に見えるはずです。
そして、4次元からみれば、3次元なんてとても窮屈に思えるに違いありません。
そこで、3次元の世界から解き放たれて、4次元の世界に旅立ってみることにしましょう。
それが下の絵です。
3次元の扉が開いて3次元から人がはみ出してきました。

このような話をすると、そんな空間本当にあるんですか?って質問をする人がいます。 この話は(一応)数学の話です。 私はそんなとき、""少なくとも数学的には""そのような空間は存在しますよって答えることにしています。 (この世の次元は3次元より大きくて、その広い世界の中に人は住んでいると言う物理学者もいます。)
数学で方向を定めるには、数直線(どこまでも長い直線)を使います。
つまり、無限の彼方まで続いている直線。
その直線には目盛がついています。0 から始まってずーっと。
一つの数は一つの目盛に対応します。
そして、3次元ではそのような方向が3つありますので、無限の目盛がついた直線を3つ用意します。
(u,v,w) という数の組を与えるとその3つの直線に沿って3次元空間上のどこかの点を表します。
u v w は3次元の住所の番地と思えます。
数学ではそれを座標と呼んでいます。
例えば、入口から3つめのを奥に4つ入ってその5階とか。

3次元だから3つある。じゃあ4次元なら、、、、、もちろん4つですね。
つまり、住所は (u,v,w,x) です。
新しく加わった方向が x というわけです。
もともとあった3次元空間 (u,v,w)を4次元空間の中に(u,v,w,0) として置きましょう。
そこから4次元の方向に少し散歩してみます。
(u,v,w,0) からでてくることにしますね。
(u,v,w,0,0001), (u,v,w,0.0002), (u,v,w,0,0003)......とそろそろ
と出てきます。 (u,v,w,1) まできました。
そして、そのあたりを少しうろうろして、 (u,v,w+0,0001,1), (u,v,w+0,0002,1), .....(u,v,w+1,1) まで来ました。
結構遠出してしまいました。
そろそろ帰りましょうか。 (u,v,w+1,0.999), (u,v,w+1,0.998),(u,v,w+1,0,997),,,,,(u,v,w+1,0,0001),(u,v,w+1,0)
やっともとの空間に戻ってきました。
あれ!最初は (u,v,w,0) から出たのにいつの間にか (u,v,w+1,0) に帰ってますね。
3次元から見れば、(u,v,w,0) で人が忽然と消えて、(u,v,w+1,0) に忽然と姿を表したことになります。
これをSFとかではワープというのでしょうか?
これはSFではなく、ただの4次元を通った散歩というわけです。
このように、4次元があれば、3次元のあらゆるところにつながるワープができることになります。
ドラえもんのポケットがスペアポケットにつながっていたのはこうしたことが行われているわけです。

このように数学があれば、ドラえもんのポケットの仕組みが簡単に説明できます。
[4次元の球体の体積と表面積]
さて、4次元の生活も慣れたでしょうか?
4次元での球体の体積と表面積を求めてみましょう。
4次元の球体とは、原点から距離 r 以下にある点の集合です。つまり、
[4次元多様体]
4次元の球体の表面積や体積が分かりました。
もう4次元ではやることはないのでしょうか。
いやいや、4次元は球体だけではありません。
実は、多様体と言われるものを考えれば、4次元はものすごく沢山あります。
そして、研究しなければ分からないことが山ほどあります。
[多様体]とは、球体を上手く繋ぎ合わせていってできる幾何学的対象のことです。
言いかえれば、多様体とはどの点を見ても局所的には球体ということです。
前回でみた、ドーナツの表面(トーラス)は、いくつか、円盤(2次元球体)を繋ぎあわせることによって作られます。
つまり、トーラスは2次元多様体です。
また、トーラスは局所的にみれば円盤ですが、全体としては円盤とは違った性質ものです。
(これをトポロジカルに違うという言い方をします。)
前回でてきた、球面も円盤を貼り合わせてできているので、2次元多様体です。
このように、4次元でも4次元の球体をいくつか繋ぎ合わせてできるものを4次元多様体といいます。
このような4次元多様体がどれほどあるのか?を探るのが4次元トポロジストの仕事です。
つまり、(いくつかの)4次元球体の繋ぎ方がどれほどあるかということを研究するのです。
4次元多様体の例
S4(4次元球面)、T4(4次元トーラス)、K3(K3曲面)、CP2(複素射影平面)、楕円曲面、一般型複素曲面、M×S1(3次元多様体と円周の直積)、双曲的4次元多様体、シンプレクティック4次元多様体、
これらの連結和や、それらをさらにトーラスで手術して得られるものetc。
実は4次元多様体は恐ろしく沢山(ある意味原理的に分類できないほど)あることが分かっています。 つまり、4次元多様体はとても複雑だということです。 また、多様体に入る大まかな幾何的性質をもつ空間(普遍被覆空間)も、分類されているわけではありません。 さらに、他の次元では見られないような面白い現象も沢山あることが分かっています (エキゾチック構造、4次元のポアンカレ予想、ユークリッド4次元空間の非可算無限個の微分構造)。 4次元にはまだまだ、分かっていないことが沢山あります。ある意味分からないことの宝の山といえるでしょう。 みなさんもトポロジーを勉強して奇妙で面白い4次元の世界に少しでも足を踏み入れてみませんか?
(6/9/2012)