数学基礎(Basic Mathematics IIA) 2011年度前期
火曜日2,3限
授業一覧に戻る
第1回(4/12)
線形性とは、用語説明など
内容:
- 線形性とはなにか?
線型とは1次のことである。そして1次式 f(x) とは次を満たす関数のことと同値である。
(ただし k は任意の実数もしくは複素数を表します。x, y はベクトルです。)
- f(x+y)=f(x)+f(y)
- f(kx)=kf(x)
- 集合と記号。(集合の表しかた。集合の演算。)
- (∀)「任意の~」と(∃)「ある~が存在して~」の使い方。
- 数学で使われる論理。(逆、裏、対偶、背理法)
- 写像。(定義といくつかの例。)
(注:上の x は1変数の x を表すだけでなく、一般にベクトル x=(x1,x2,…,xn) などを表します。)
第2回(4/19)
写像の続き、複素数。
- 写像の合成、像、逆像の定義。
- 直積集合の定義。
- 単射と全射と全単射。
- 単射、全射、全単射、全射でも単射でもない例。
- 集合の濃度。
- 数学的に数えるとはどういうことか?
- 複素数の構成。
(実数と虚数単位 i を含み、"実数と同じ計算規則"をもつ集合を作ること。)
- a+bi の形をしたものに次の足し算と掛け算を導入する。
- (a+bi)+(c+di)=(a+c)+(b+d)i
- (a+bi)(c+di)=(ac-bd)+(ad+bc)i
- このとき、割り算も一意的にできる。
- 体の定義。
- 複素数は体の条件("実数と同じ計算規則"をもつ)を満たす集合である。(実数と同じ性質を満たす。)
- 体の条件を満たすものは他に実数、有理数などがある。(もちろん数学の世界では其れ以外にもある!)
- 整数全体は体にはならない。(なぜか?)
- 複素数の極座標表示。
第3回(4/26)
複素数の掛け算。1のべき乗根。数ベクトル空間。
- 複素数 z=r(cosθ+isinθ) の掛け算とは原点を中心とした r 倍と θ 回転を表す。
- ドモアブルの公式
(cosθ+isinθ)^n=cos(nθ)+isin(nθ)
- 複素数を用いた三角関数の加法定理の証明。
- 複素共役について。
- Re(z)=(z+z*)/2, Im(z)=(z-z*)/(2i), (z* は z の複素共役)
- 複素共役の性質(1)(2)(3)
- 1の n 乗根
- 1の n 乗根は複素平面上の単位円上にあり1を基準に n 等分点になっていること。
- 1の n 乗根は丁度 n 個あること。
- 演習
- 1 の 5 乗根を求めよ。
- 半径 1 の円に内接する正五角形の一辺の長さを求めよ。
- 数ベクトル空間の定義。
- 数ベクトル空間の性質。
第4回(5/10)
行列登場。
- 複素数の復習zn=aの方程式の解き方。
- 行列の定義。
- 第 i 行, 第 j 列, 第 i,j 成分。
- 行列の加法、スカラー培。
- 行列の積とは何か?
-
 上に(x1,x2,...,xn)を変数とするしたのような1次式を考えます。
上に(x1,x2,...,xn)を変数とするしたのような1次式を考えます。

- 以下のように

1次式を行列とベクトルの積のように表します。
- こうすると右辺が本当の積のように表されて、行列をAとすると
Axとなること。
- y=Axは数ベクトル空間から数ベクトル空間への写像を表すこと。
 となります。
となります。- 数ベクトル空間上の1次式は線形性を満たすこと。(線形性をもつ写像のことを線形写像と呼びます。)
- よって、y=Axは上記の線形条件を満たす。
- 合成に関しては
 の等式が成り立ちます。
の等式が成り立ちます。
- ∵fAとfBの合成も線形写像であり、f*とかけます。この*をBとAの積として定義するわけですね。
- 当然ですがfA終域とfBの始域は一致しないと写像の合成は定義できません。つまり行列の積も定義できません。特に数ベクトル空間の次元も同じです。
- 行列の積は

となります。
第5回(5/17)
行列の簡約化と連立一次方程式。
- 連立一次方程式の復習(代入法と加減法)。
- 行に関する基本変形
- ある行を定数倍する。
- 2つの行を入れ替える。
- ある行に他の行の定数倍を足す。
- 基本変形は連立一次方程式を加減法だけを使って解く時のプロセスである。
- 階段行列。その主成分。
- 主成分が1で主成分のある列で主成分以外の成分は全て0である行列を簡約(な)行列という。
- 行列の簡約化。
- 連立一次方程式への応用。
- 拡大係数行列。
- 拡大係数行列を簡約化することで、連立一次方程式を解くこと。
- 演習。
レポート問題の配布。
以下のレポートを解いて、レポートボックスに提出してください。
レポート問題
レポートボックスは来週作る予定です。
第6回(5/24)
基本行列、逆行列
- Ax=b の解 x は Ax0=b となるある解と、Ay=0 の解の和として x=x0+y とかけること。
- (1)Aをm×n行列ならば Ax=0 に自明でない解を持つための必要十分条件は rank(A)=n であること。
(2)とくに m< n ならば、 Ax=0 には非自明な解が存在する。
- 基本行列 I(i,c), II(i,j), III(i,j,c) の定義
- 行の基本変形はそれぞれ基本行列の左からの積で書きあらわされること。
- 逆行列の求め方。
- 演習。
(5/31)
休講
第7回(6/7)
行列式
- 正方行列はいつ逆行列をもつか?について
- 正方行列 A が逆行列をもつことと、連立一次方程式 Ax=0 が自明な解 x=0 しか持たないことは同値である。
- 正方行列 A が逆行列をもつことと行列の rank がフルランク(行列のサイズと同じ)であることは同値である。
- n 次対称群 Sn の定義。
- Snは自然に積が入り、逆元が存在すること。単位元が存在すること。
- 群の定義。
- 互換と巡回置換。
- 任意の置換は巡回置換の積でかけること。
- 任意の巡回置換は互換の積で書けること。
- 任意の置換は互換の積で書けること。
- 置換の符合の定義。
- 置換を互換での表し方は一意ではないが、符合の値はどの表し方でも同じ値になること。
- 行列式の定義。
- 基本変形したときの行列式の変化
- det(I(i,c)A)=cdet(A)
- det(II(i,c)A)=-det(A)
- det(III(i,c)A)=det(A)
- 行列式が 0 でないことは行列に逆行列が存在することと同値であることの証明。
第8回(6/14)
サラスの方法、行列式の展開
- 3×3行列の行列式の公式(サラスの方法.)
- 行列のうち2つの行が同じベクトルであるとき行列式は0になること.
- 1行目が (a11,0,....,0) である行列の行列式について.
- 行列式の余因子展開.
- 行列が正則であるためのいくつかの同値条件.
第9回(6/21)
正則行列のいくつかの言い換え。余因子行列。
- 余因子行列.
- 逆行列は(余因子行列)/det(A)であること.
- 行列式の公式1 det(tA)=det(A) (転置行列の行列式)
- 行列式の公式2
 =det(A)de(D) (A,Dは正方行列)
=det(A)de(D) (A,Dは正方行列)
- 行列式の公式3 det(AB)=det(A)det(B)
- 行列式の演習.
第10回(6/28)
クラメルの方法.ファンデルモンテの行列式.
- 連立方程式(III) クラメルの方法
- Ax=b をクラメルの方法を用いて解く方法.
- ファンデルモンテの行列式の証明.
- 演習問題の配布.
第11回(7/5)
巡回行列式.演習.
演習の回答状況
火曜日2限
1,2,3,6,8(1),11
火曜日3限
1,2,3,5(1,2,4),6,8(1,2,4),9(1,2,3),11(1,2),25(1,2),27(1,2,3,4),28,30(1,3,6),31,34(1,2),35(2),37
第12回(7/12)
面積・体積、演習
- 2×2行列の行列式はその行列をつくる2つのベクトルからなる平行四辺形の面積に等しいこと。
- 3×3行列の行列式はその行列をつくる3つのベクトルからなる平行六面体の面積に等しいこと。
- 2つの3次元ベクトルの外積。
- 外積はその2つのベクトルに直交すること。
- 外積の長さはその2つのベクトルからなる平行四辺形の面積に等しいこと。
- 演習。
(7/19)休講
第13回(7/26)定期試験
試験問題
解答例
第14回(8/2)
線形計画法。演習。
コメント
この欄は、質問を受けた個所や、授業で言い忘れたことなどを補足しておきます。
メール(アドレスは下に記載)での質問も受け付けます。
☞線型について
- 線型方程式とはAx=bを満たす方程式のことです( A は行列, x , b はベクトル)。
これを x について解く理論が線形代数です。
☞必要・十分条件について
- A, B をある条件とします。
そのとき、 A⇒B という命題があったときに、A のことををBが成り立つための十分条件。
Bのことを A が成り立つための必要条件と言います。
- 例として
人間である ⇒ 動物である
という命題があったとします。
この命題では、人間であることは動物であることの十分条件であり、動物であることは人間であることの必要条件と言えます。
- A⇒B かつ B⇒A であれば、A は B が成り立つための必要条件であり、十分条件と言えます。
このようなとき、A と B は必要十分条件であるいいます。( A と B は同値(条件)であるとも言います。)
☞記号について
- 等式を含む意味の不等号は ≤ や ≥ の方を大学ではよく使います。
- ベクトルを表す時、記号( x など)の上に→を書いたりしましたが、大学では x のように太文字(ボールドフォント)にすることがあります。
☞写像について
- 写像 f:A→B は、A, B を集合として、任意の A の元 x に対してただ一つ B の元 y を選ぶ操作のことです。
- 10人以上からなる野球部の監督がスタメンを選ぶ操作は写像にはなりません。(∵選ばれないものが1人以上はいるから)
- 野球部監督がメンバーを1軍と2軍に分ける操作は以下のように写像になります。
f:{メンバー} → {1,2}
☞cos(2π/5)の値について。
- cos(4π/5)=cos(6π/5)が成り立ちます。
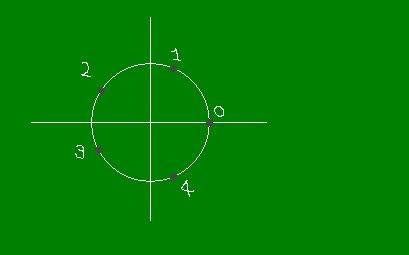
下の単位円上の5等分点の2つめと3つめの実座標が等しいですよね。
つまり両者は複素共役。
- cos(4π/5)=2cos²(2π/5)-1 (2倍角の公式)
- cos(6π/5)=4cos³(2π/5)-3cos(2π/5) (3倍角の公式)
- t=cos(2π/5)とおき、3次方程式を解く。
- sin の方の計算も同じ考え方を使いましょう。
☞[!発展!] z5-1=0の解について
- z⁵-1=0を解いて実部を取ることで cos(2π/5) を計算することもできます。
- この方程式を解くのは少し難しいです。(2次方程式を2回解くことになるので少しマニアックです。)
- まず (z-1)(z4+z3+z2+z+1) と因数分解します。
- z=1 もしくはz4+z3+z2+z+1=0が解ですが、後者を考えます。
- このとき、z≠0 ですから、z² で割って z²+z+1+(1/z)+(1/z)²=0 とします。
- この式は w=z+1/z の2次方程式として書き直せます。
- よって解の公式を使って w を解きます。
- その値を使って z²-wz+1=0 の方程式を解の公式を使って解きます。
- [余談] なぜこの4次方程式は2次方程式を2回解くことに帰着するのか?
実は数学的な理由があります。(→ガロア理論)
☞ギリシャ文字について
数学では文字の式の時にギリシャ文字がよく登場します。
ここで紹介しておきます。左は大文字、右は小文字。
- Α、α(アルファ)
- Β、β(ベータ)
- Γ、γ(ガンマ)
- Δ、δ(デルタ)
- Ε、ε(エプシロン)
- Ζ、ζ(ゼータ)
- Η、η(エータ)
- Θ、θ(テータ)
- Ι、ι(イオタ)
- Κ、κ(カッパ)
- Λ、λ(ラムダ)
- Μ、μ(ミュー)
- Ν、ν(ニュー)
- Ξ、ξ(グザイ)
- Ο、ο(オミクロン)
- Π、π(パイ)
- Ρ、ρ(ロー)
- Σ、σ(シグマ)
- Τ、τ(タウ)
- Υ、υ(ユプシロン)
- Φ、φ(ファイ)
- Χ、χ(カイ)
- Ψ、ψ(プサイ)
- Ω、ω(オメガ)
☞代数学の基本定理
複素数係数をもつn次多項式の根には必ず、複素数の範囲で丁度n個の解をもつという定理を
代数学の基本定理と言います。
ただし、重解や3重解はそれぞれ、2個や3個などと解の数を数えます。
歴史的にはガウスが初めてこの定理の厳密な証明に成功しました。
実数係数の多項式は実数上でいつも解があるとは限りません。
例えば、 x²+1=0 は実数係数多項式ですが実数では解を持ちません。
☞複素数についての注
実数は複素数に含めないと勘違いしている人がいますが、実数も複素数の特殊な場合(a+0i∈C)なので、
立派な複素数です。
☞n次対称群 Sn (エスエヌ)
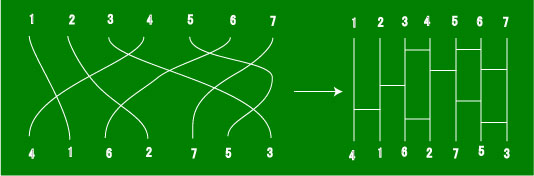
n次対称群というものを授業で紹介しましたが、これを簡単に理解する方法があります。
それがあみだくじです。
授業で例として挙げた下のような置換を考えましょう。
上に数字 1,2,...,n をおき、下に、置換された値を置きます。
それらを同じ数字同士を線で結びます。
その線を交点の周りで少し平らにして、他の部分を
上下にぴんと張ると右のようなよく見るあみだくじが現れます。
一般に、あみだくじとは、左のようなヒモの集まりと考えてよいでしょう。
縁日で見かける紐引きや結婚式で行われるブーケプルズはあみだくじと
考えられます。
置換とはこのような、上下に配置された同数個の点を線分で結んだものとして理解できます。
逆にこのような線分があれば置換が1つ与えられることは言うまでもありません。
これが置換の幾何学的イメージです。
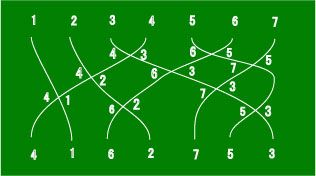
結んだ線上にも対応する数字を与えることにしましょう。
上で書いた線分達の交わる交点で、与えられた数字が交換されていることに注意してください。
例えば一番左の交点は 1 と4 に対応する線分の交点ですがその交点の上下で 1 と 4 の
左右の位置が入れ替わっています。
これらの数字の交換は実は互換に対応します。
この絵はこのような線分の入れ替えの複合によって成り立っていることがわかります。
つまり、置換が互換の積でかけていることをこの絵によって説明しているわけです。
上のように、交換された数字をその下に書いていき、その交換をそのまま
互換として右から並べていくと
(3,5)(3,7)(2,6)(4,1)(4,2)(6,3)(5,7)(6,5)(4,3)
と書けることがわかります。(確かめよ。)
交点同士の上下関係が積の右左関係になるように順番を保ってください。
ちなみにこの置換の符合は (-1)9= -1 となることもすぐわかります。
9 は交点の数です。
結局符合とはこうして書いた交点の偶奇を求めていることに他なりません。
☞置換の符合について
授業中で置換の符合は互換の表し方によらないことを言いましたがこの場で、それを以下のように説明しましょう。
まず、
σ=( i 1, j 1 ) ( i 2, j 2) .... ( i p, j p )
σ=( k 1, l 1 ) ( k 2, l 2) .... ( k q, l q )
のように置換σ∈Snが互換の表し方として2通りあったとします。
このとき、
σσ-1=( i 1, j 1 ) ( i 2, j 2 ) .... ( i p, j p )( k q, l q ) .... ( k 2, l 2 ) ( k 1, l 1 )=e
となりますが、これは恒等変換つまり単位元です。
つまり、単位元 e がある p+q 個の互換で表されたことになります。
ここで、 p+q が奇数であるとして矛盾を導きます。
( p+q が奇数であるとすると、p と q の偶奇は一致しなくてσの符合が互換の表し方によってしまうことになります。)
p+q=R と置きなおし、さきほどの互換の積を改めて
e=τ1 τ2 ... τR
とします。
このとき、1つの互換 ( i , j ) は下のようなあみだくじに対応します。
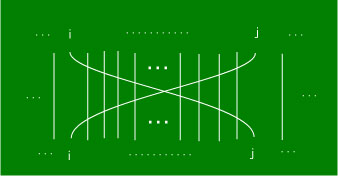
i と j が入れ替わり、その他はまっすぐ下に降りているのがわかるでしょうか。
このあみだくじでは、線分の交点は奇数個です(中央に i と j の交わりの1点と、i と j の間の線分と2本ずつ交わっています)。
表示
e=τ1 τ2 ... τR
が表す互換の積をこの絵を用いて表すと、このあみだを縦に R 個並べることになります。
そうすると交点は全部で R×(奇数) でやはり全ての交点は奇数個です。
この置換は全体として単位元であることを思い出しましょう。
つまり、線分をたどると、1, 2, .... , n はこの順番の通りに戻ってきます。
ここで、任意の0≤ i< j≤nをとります。
2つの線分 i, j もやはり、単位元による変換で i→i, j→j となっていますがその間の交点は必ず偶数個です。
つまり、一方の線分が一方の線分を超えた場合、もう一度またぎ直さないと元の位置に戻ってこれないからです。
よって、このことは任意の相異なる i と j について言えますから、
交点の総数は偶数個になります。
これは上に書いたことから明らかに矛盾します。
よって、 R は偶数でなければならないことになります。
このことによって、σ を互換の積として表したとき、その互換の数の偶奇はいつも一定であることがわかりました。
この一定の偶奇を用いて、置換σの符合を定義していたわけです。
☞列に関する基本変形
授業では行に関する基本変形を定義しましたが、列に関する基本変形も同様にあります。
- ある列を定数倍(c倍)する。
- 2つの列を入れ替える。
- ある列に他の列の定数倍を加える。
列に関する基本変形は基本行列の右からの積に対応します。
対応して行列式の変化は次のようになります。
次に列の基本変形も混ぜて行列を階段行列にします。
まず任意の行列 A を行に関する基本変形をします。
そうすると A は XA に移ります。
X はいくつかの基本行列の積で、XA は簡約行列です。
さらにこの行列を列に関する基本変形を行います。
行列は XAY となります。
Y は基本行列のいくつかの積です。
こうすることで XAY は階段行列で、主成分以外全て 0 の行列にすることができます。
ここで注意したいことは、連立方程式を解く場合は列の基本変形を使ってはいけないということです。
列を基本変形すると変数 x1,x2,...,xnがずれてしまい、最終的に
(x1,x2,...,xn)=(a1,a2,...,an) という形で
求まらなくなってしまいます。
☞全射と単射
全射と単射をここで説明します.
全射と単射を分かる前に写像の定義はわかっていますか?
もう一度繰り返すと、
写像 f とは、全ての A の元 a に対してただ一つ B の元 f(a) を対応させる規則のこと.
を言います.
全射と単射が分かっていない人の半数が写像の定義がきちんとわかっていません.
これが分かった上で、
[単射とは]
写像 f:A→B であって、A の違う元が同じ B の元に行くことはないことである.
つまりもし、x1とx2が B 同じ元 f(x1)=f(x2) に行くとすると
x1=x2である.
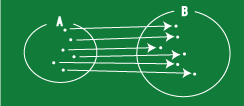 ]
]
A の元は B に行ったときに重ならない.
[全射とは]
写像 f:A→B であって、全ての B の元は f からの像として A から来ている.
つまり、任意の B の元 b はある A の元 a が存在して f(a)=b となる.
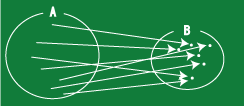
B の全ての元に A から来ている.
ただ、A から同じ元に行っていてもよい.
授業一覧に戻る
tange (あっとまーく) kurims.kyoto-u.ac.jp
(あっとまーく)=@
 上に(x1,x2,...,xn)を変数とするしたのような1次式を考えます。
上に(x1,x2,...,xn)を変数とするしたのような1次式を考えます。

 となります。
となります。 の等式が成り立ちます。
の等式が成り立ちます。
 上に(x1,x2,...,xn)を変数とするしたのような1次式を考えます。
上に(x1,x2,...,xn)を変数とするしたのような1次式を考えます。

 となります。
となります。 の等式が成り立ちます。
の等式が成り立ちます。
 =det(A)de(D) (A,Dは正方行列)
=det(A)de(D) (A,Dは正方行列)



 ]
]
